
Version LX
SPRACHE
Zahlensysteme der Antike

![]() GRIECHENLAND I
GRIECHENLAND I
![]() GRIECHENLAND
II
GRIECHENLAND
II
Allgemeines
Bereits um 450 v.Chr. wurde das herodianische System durch die alphabetische Zahlenschrift ergänzt, doch erfolgte eine verbindliche Verwendung in Athen erst in römischer Zeit um 50 n.Chr.
Die Zuweisung der Zahlenwerte zu den Buchstaben dürfte jedoch bereits
im 8.Jhv.Chr. in Milet erfolgt sein. Danach hielt es sich über die Antike hinweg bis ins 15.Jh.n.Chr., ehe sich die indische Stellenschreibweise mit einem Punkt für die Null durchzusetzen begann. Da auf Anhieb Zahlen von Wörtern nicht unterschieden
werden konnten, machte man über Zahlen oft einen Querstrich.
Man verwendete das vorhandene griechische Alphabet nebst den drei erhalten
gebliebenen semitischen Zeichen Digamma, Koppa und San, was in Summe 27 Zahlzeichen ergab.
Für das San gab es allerdings verschiedene Darstellungsformen, so
u.a. auch ein Pfeil nach oben. Die
Werte von eins bis neun, 10 bis 90 sowie 100 bis 900 wurden der Reihe nach den Buchstaben wie folgt zugeordnet:
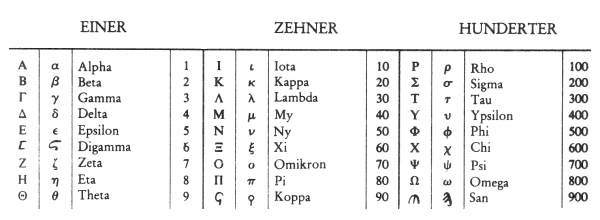
Die Zahlen wurden nun durch Addition der einzelnen Zeichen gebildet. ,ροε steht etwa für 175. Damit konnte man Werte bis 1000 darstellen. Um Beträge darüber schreiben zu können, verwendete man einen kleinen Strich links unterhalb (manchmal auch oberhalb) eines Buchstabens und zählte erneut von vorne mit dem Faktor 1000 durch, was das System bis zu 900.000 erweiterte. Beispiel: ,ρ,οε steht nun für 170.005. An diesem Beispiel erkennt man, dass sorgfältiges Schreiben unerlässlich war, um nicht gleich in ganzen Potenzen eine Fehlinterpretation zu verursachen.
Die Alphabetzahlen verbreiteten sich mit der griechischen Kolonisierung im ganzen Mittelmeerraum und waren auch für angrenzende Völker von enormer Wichtigkeit (z.B. Ägypten, Mesopotamien, Naher Osten). Wie die lateinischen Buchstabenziffern im Westen hielt sich die griechische Zählweise im Osten des Mittelmeers bis ins Mittelalter. Hier ein Beispiel für die Koptischen Zahlzeichen:
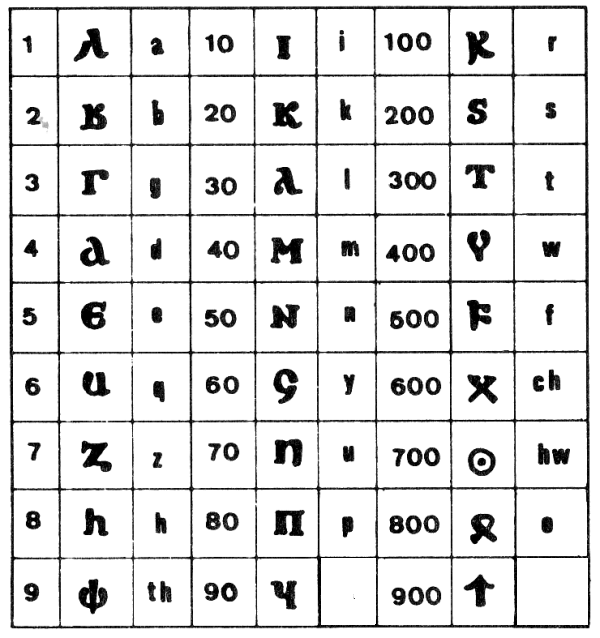
Wirklich grosse Zahlen im alphabetischen Ziffernsystem
Um noch grössere Zahlen darstellen zu können, wurden verschiedene Verfahren angewendet. Die wichtigste war die Zählung nach Myriaden (10.000er). Über dem Zeichen M schrieb man jene Zahl, die mit 10.000 zu multiplizieren war. Damit waren Zahlen bis 100 Millionen darstellbar. Die Zählung nach Myriaden war weitverbreitet und erfuhr im Laufe der Zeit manche Abwandlung. Aristarchos von Samos schrieb Mitte des 3.Jh.v.Chr. die zu multiplizierenden Zahlen links vom M, die hernach zu addierenden Zahlen rechts davon:
’ζροε Μ ’εωοε = 7175 x 10.000 + 5875 = 71.755.875
Ein halbes Jahrtausend später hatte Diophantos von Alexandria das M durch einen Punkt ersetzt, was bei ihm so aussah (er verwendete allerdings anstatt des Theta ein anders Symbol):
δτοβ
. ’ηθζ = 4372 x
10.000 + 8097 = 43.728.097
Der Mathematiker und Astronom Apollonios von Perge schlug Anfang des 2.Jh.v.Chr. ein System vor, das auf den Potenzen der Myriade beruhen sollte. Die Zahl über dem M wäre dann die jeweilige Potenz von 10.000 (erste Myriade, zweite Myriade, etc.). Damit liessen sich auch sehr grosse Zahlen darstellen. Die Myriaden wurden mit dem Wort kai (= plus) verbunden. Aus einem Papyrus des 3.Jh.n.Chr. kennt man etwa folgende Zahl:
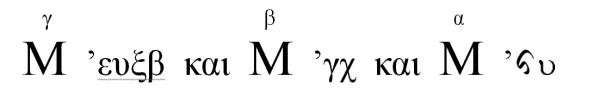
Dies sind 5462 dritte Myriaden, 3600 zweite Myriaden und 6400 erste Myriaden (das vorletzte Zeichen ist ein Digamma), was die Zahl 5.462.360.064.000.000 ergibt; also gut fünfeinhalb Billiarden. An diesem Beispiel ist auch der schleichende Einzug des Stellenwertsystems zu erkennen. Sicher den Vogel abgeschossen hat allerdings Archimedes, der ein Zahlensystem ersann, das alles andere in den Schatten stellte. Er erweiterte die Myriaden zu Oktaden, was nicht nur 10.000 sondern 100 Millionen Zahlen pro Potenz erlaubte. Damit beschrieb er eine Zahl mit 64 Millionen Nullen! Da selbst die damaligen Mathematiker meist mit wesentlich geringwertigeren Zahlen ihr Auslangen fanden, setzte sich das archimedische System nicht durch.
Rechnen mit alphabetischen Zahlzeichen
Das alphabetische System eignete sich ausgezeichnet für das schriftliche Rechnen. Rechenzeichen und Abstände zwischen den Zahlen gab es in der Antike nicht und die gewählte Operation musste aus dem Text erschlossen werden. Um die Sache zu vereinfachen gab es Additions- und Multiplikationstabellen, wo man einfach die Buchstaben in einem Raster suchte und das Ergebnis bereits vorgerechnet vorfand (sozusagen die primitivste Form des Taschenrechners).
Bruchrechnen war im alten Griechenland bereits im 5.Jh.v.Chr. gang und gäbe. Oft wurden gar keine Zahlen verwendet, sondern die Brüche in Worten ausgeschrieben. Für die Werte halb und zwei Drittel gab es eigene ZeichenBei Zahlzeichen machte man für Stammbrüche bei einem Zahlzeichen rechts oben einen oder zwei kleine Striche. Allgemeine Brüche mussten (wie bei den Ägyptern) in Stammbrüche zerlegt werden, damit sie dargestellt werden konnten. Also behalf man sich mit der Hintereinanderschreibung von Zähler und Nenner. Da sich dies auch als unpraktisch erwies, entwickelte man bereits eine der modernen Schreibung ähnliche Form mit dem Zähler über dem Nenner; allerdings ohne Bruchstrich. Ab dem 1.Jh.n.Chr. vertauschte man Zähler und Nenner, was sicherlich zu einigen Leseschwierigkeiten geführt haben dürfte. In einigen Spezialdisziplinen, wie etwa der Astronomie, verwendete man Normbrüche auf 60stel, 120stel oder 360stel und kennzeichnete sie mit kleinen Strichen rechts oberhalb der Zahl. Auf diesem System beruht noch heute in der Geografie die Schreibung nach Minuten und Sekunden bei Ortsangaben.

Römische Wachstafel
mit Griffel
Quellen: G.Ifrah "Universalgeschichte der Zahlen", H.Pleticha & O.Schönberger "Die Griechen"
Sie wollen Fragen stellen, Anregungen
liefern oder sich beschweren?
Dann klicken Sie auf meine Kontaktseite!
(PL)
